Définition
Comme décrit dans l’article Les cadences, la cadence parfaite est un enchainent de deux accords qui conclut une phrase musicale (dans la musique tonale), cette cadence donne une impression de quelque chose qui se termine. Par convention dans le langage de la musique tonale, la cadence parfaite est une cadence conclusive.
L'enchainement d'accord pour la cadence parfaite est le suivant :
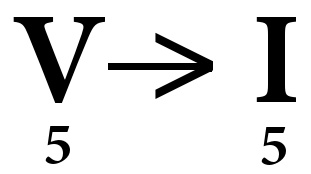
Pour qu'une cadence soit parfaite, il y a deux conditions indispensables :
- Enchainement du degré V vers le degré I
- Les deux accords sont à l'état fondamental (le chiffre arabe 5 est le chiffrage d'accord de l'accord parfait à l'état fondamental)
Les cadences V-I (parfaite et imparfaite) sont aussi nommées cadences authentiques, vous trouverez parfois les termes de cadence authentique parfaite et de cadence authentique imparfaite.
Cadence italienne (cadence complète)
La cadence italienne, aussi intitulée cadence complète est une cadence parfaite amplifiée, et consiste dans l'enchaînement des degrés IV, V et I. Le degré II peut remplacer le degré IV (II V I) ou s'ajouter à l'enchainement (IV II V I), ce dernier enchaînement est très courant et on le retrouve même dans l'hymne français La Marseillaise.
L'enchainement d'accord pour la cadence italienne (cadence complète) est le suivant :
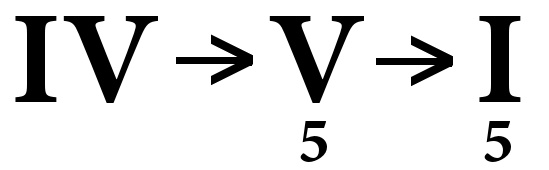
Ou bien :
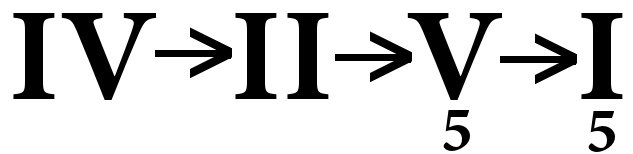
Ce qui importe dans la cadence complète, c'est l'enchainement V / I, les autres degrés sont des degrés qui préparent l'arrivée de la cadence parfaite.
Cadences parfaites avec accord de septième de dominante
L'accord de septième de dominante est très souvent utilisé dans les cadences parfaites :
Les accords de septième de dominante sont des accords à 4 sons, basés sur l'accord de dominante (degré V) et qui comportent des mouvements obligés :
L'intervalle de septième doit se résoudre en baissant d'un degré (la note septième descend).
Les intervalles augmentés doivent se résoudre en augmentant d'un degré (vers un intervalle plus grand).
Les intervalles diminués doivent se résoudre en baissant d'un degré (vers un intervalle plus petit).
Vous remarquerez que dans l'exemple ci-dessus, la dernière cadence est une cadence imparfaite.
Exemples de cadence parfaites
Symphonie n° 41 de Mozart
Exemple de cadence parfaite dans le Trio du menuet de la Symphonie n° 41 en ut majeur KV. 551 de Wolfgang Amadeus Mozart :
Cet extrait est en DO Majeur et les degrés V et I sont respectivement :
degré I : DO / MI / SOL (accord parfait de DO majeur)
degré V : SOL / SI / RÉ (accord parfait de SOL majeur)
L'automne de Vivaldi
Exemple de cadence parfaite dans le mouvement L'automne, extrait des quatre saisons de Vivaldi :
Cet extrait des quatre saisons est en FA Majeur et les degrés V et I sont respectivement :
degré I : FA / LA / DO (accord parfait de FA majeur)
degré V : DO / MI / SOL (accord parfait de DO majeur)
Jesu, meine Freude de J.S. Bach
Le choral Jesu, meine Freude BWV 227 de Johann Sebastian Bach, comporte une tierce picarde dans la cadence parfaite entre les mesures 12 et 13 :
Extrait libre de droit enregistré par le Stuttgarter Hymnuschorknaben et le Stuttagarter Bachorchester sous la direction de Wilhelm Gerhard (source, licence Non-PD US)
La Marseillaise
La Marseillaise comporte une cadence italienne (cadence complète). Cet extrait est en SOL Majeur et les degrés IV, II, V et I sont respectivement :
degré I : SOL / SI / RÉ (accord parfait de SOL majeur)
degré II : LA / DO / MI (accord parfait de LA mineur)
degré IV : DO / MI / SOL (accord parfait de DO majeur)
degré V : RÉ / FA♯ / LA (accord parfait de RÉ majeur)
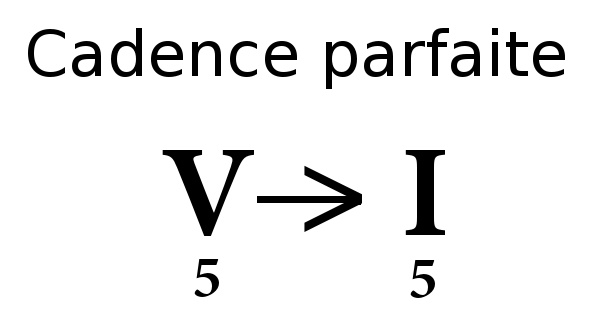
Un peu de théorie ne fait pas de mal après avoir arrêté le solfège depuis deux ans... X D
Répondre à ce(s) commentaires(s)